Writers often refer to software modelling in general terms, not distinguishing between analysis and design models. This may be ok for some purposes, since the two have a lot in common. However, there are also significant differences that need to be taken into account when studying collaboration, language engineering or tool design in software modelling.
Domain Specific Language
The language of analytical modelling is inherently domain specific. Analysis means close communication with business domain stakeholders. Thus, the primary objective of a modelling language is to foster this collaboration, and so things like obeying standards becomes secondary. ‘This is UML conformant’ is not an argument in this context.
However, it is not necessary to reinvent the wheel in every software project. Basic language elements are almost always the same, like processes with steps and flow control, entities with relationships like whole-part or generalization, states with events and transitions or systems with components and interfaces. It is hard to say, therefore, whether stereotyping is sufficient or a DSL (based on foundational elements) is required.
Moreover, the business domain unfolds during the analysis process and so does the language. Thus, an analytical modelling language is not firstly defined and then secondly used. Rather, it develops step by step as the understanding of the business domain matures.
Formality and Fuzziness
A model is at the core of each analysis in software development. One has not really understood the subject until he/she is not able to build a model of the essential process, entity structures, system parts, etc.
However, although a model itself is a quite well-structured thing, the path of getting there is usually not. It involves taking notes of ideas or approaches in an unstructured way or the (temporary) use of other models that are outside the scope of the actual analysis. Modelling in software analysis can go all the way from napkin scribble to formal model. Where it starts is strongly dependent on the business domain, its maturity, its knowledge sources, etc.
Moreover, analysis models are about understanding. They are made for humans, and since human understanding is not a straightforward thing it might be highly beneficial to enrich the model with some non-formal or narrative elements, in order to be more concrete, to refer back to common terms, for a more presentable appearance, to guide the reader or to bypass shortcomings of the modelling language. Therefore, an analysis model, although clear and precise at the core, might become fuzzier towards the paring.
Heterogeneous User Group
The stakeholders in analysis comprise a broad circle, from very different departments, workplaces, responsibilities or levels of involvement in the project. This brings up the more technical issue of providing access to the model. The stakeholders read, verify, comment, edit and navigate the model via some modelling tool they have installed in their workplace, some lightweight or browser-based utility, some common intranet, or via documents extracted from the model and sent to them by email. Of course, all this needs to be done in a way that keeps the model consistent and modifiable, which is always a considerable challenge.
Views, Views, Views
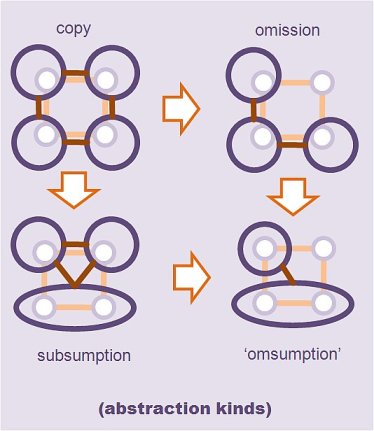
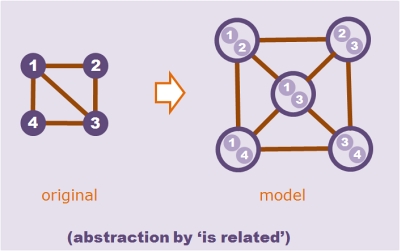
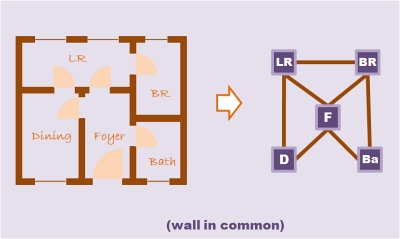
Analysis in software development is basically about understanding, and the main key to understanding is seeing things from appropriate perspectives, i.e., creating views on the model. Views are more than just reductions of the model, views are reductions that make sense – in other words, abstractions. For example, simply picking some entities with their relations from an ER-model without giving further reasoning for the choice and drawing a diagram from it is just reduction (and contributes little to nothing to understanding). As opposed to providing a rule (query) that defines the choice of the diagram and thus conveys understanding.
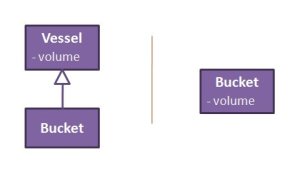 Moreover, a view contains more than just a subset of the objects of a model. It can affect its relations as well. For example, a model containing a class vessel with an attribute volume and a subclass bucket (by generalization relation), may appear in a diagram as just the bucket class with the attribute volume in it. Notice that here, the view refers to the semantics of the modelling language.
Moreover, a view contains more than just a subset of the objects of a model. It can affect its relations as well. For example, a model containing a class vessel with an attribute volume and a subclass bucket (by generalization relation), may appear in a diagram as just the bucket class with the attribute volume in it. Notice that here, the view refers to the semantics of the modelling language.
Last but not least, views create redundancy, which affects modifiability. However, handling this kind of redundancy by separating object from presentation is the core capability of modelling tools. So, this can easily be solved by tools, as long as they are capable of handling the other aspects (‘sense’, semantics) of views.
All of the above properties – domain dependence of language, structured/ unstructured mix, broad audience, and the importance of views – are surely beneficial in software design models, too, but surely do not have such a prominent role there as they have in analysis.
So long,
|=
P.S.
Dear language and tool designers – do you think you’re fit for software analysis modelling?


 from attaching accepted and meaningful names to objects and relations in the business domain so that they can easily be referred to, through defining appropriate abstraction layers for discussing and deciding on technical architecture, to agreeing on basic notions, such as what is a requirement at all, where does the biz domain model end and the technical architecture start and what are the consequences for project roles and responsibilities. And it doesn’t matter what some book or standard says. In the end, the project itself should decide which concepts or approaches to adopt or to define.
from attaching accepted and meaningful names to objects and relations in the business domain so that they can easily be referred to, through defining appropriate abstraction layers for discussing and deciding on technical architecture, to agreeing on basic notions, such as what is a requirement at all, where does the biz domain model end and the technical architecture start and what are the consequences for project roles and responsibilities. And it doesn’t matter what some book or standard says. In the end, the project itself should decide which concepts or approaches to adopt or to define.
















 The epistemic foundations of engineering recognize the concept of a technical artefact, as an intentionally produced thing, such as a piggy bank, paper clip, cell phone or dog collar. This does not apply to a physical object that unintentionally or coincidentially does something. For example, a physical object that carries out arithmetic is not by itself a calculator [SEP]. So, the technical artefact brings together the notion of the world as physical objects with the notion of intentionally acting agents, e.g., raising the hand in a meeting has physiological causes, as well as social reasons; see generally mind-body problem [Wik].
The epistemic foundations of engineering recognize the concept of a technical artefact, as an intentionally produced thing, such as a piggy bank, paper clip, cell phone or dog collar. This does not apply to a physical object that unintentionally or coincidentially does something. For example, a physical object that carries out arithmetic is not by itself a calculator [SEP]. So, the technical artefact brings together the notion of the world as physical objects with the notion of intentionally acting agents, e.g., raising the hand in a meeting has physiological causes, as well as social reasons; see generally mind-body problem [Wik].